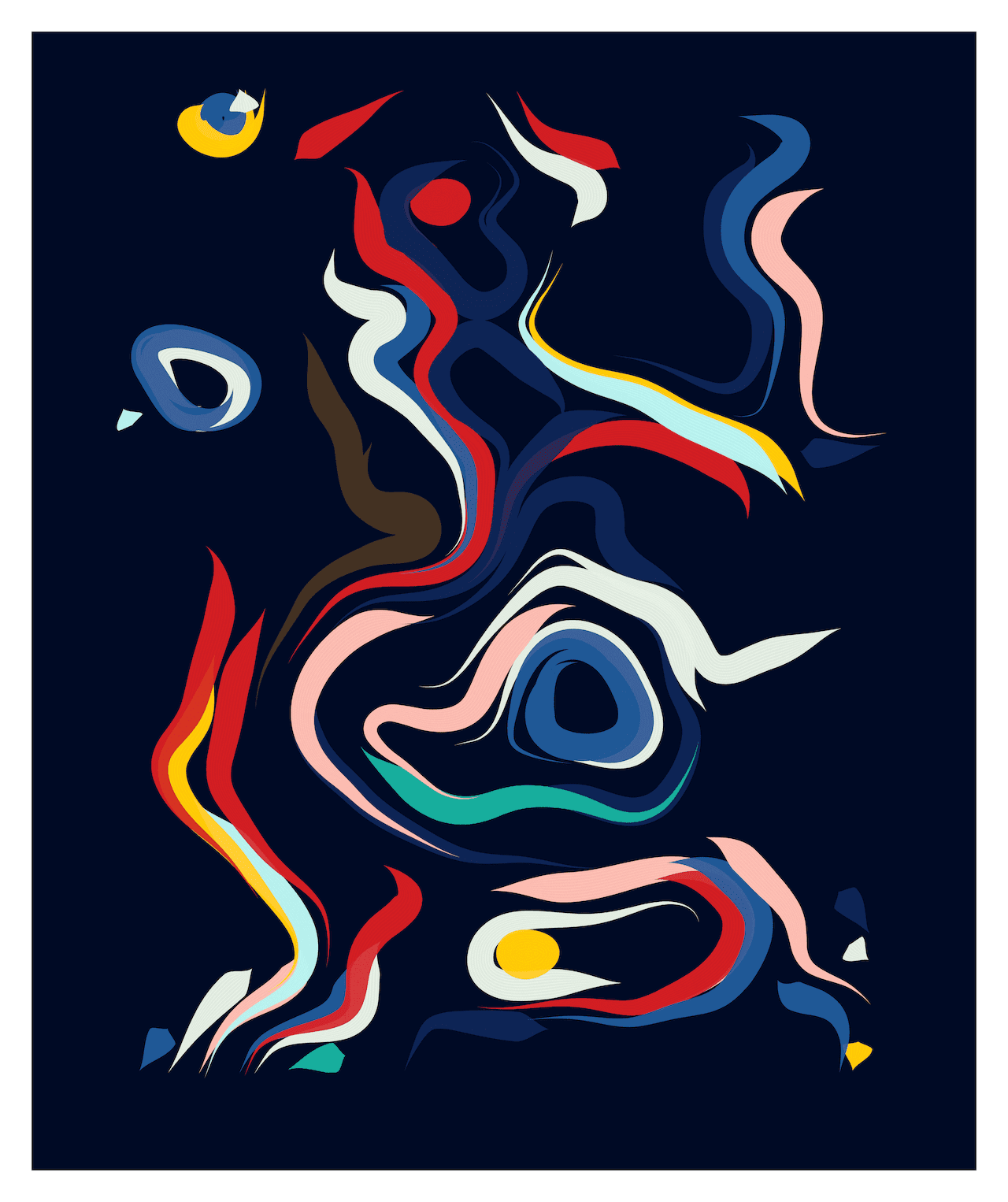
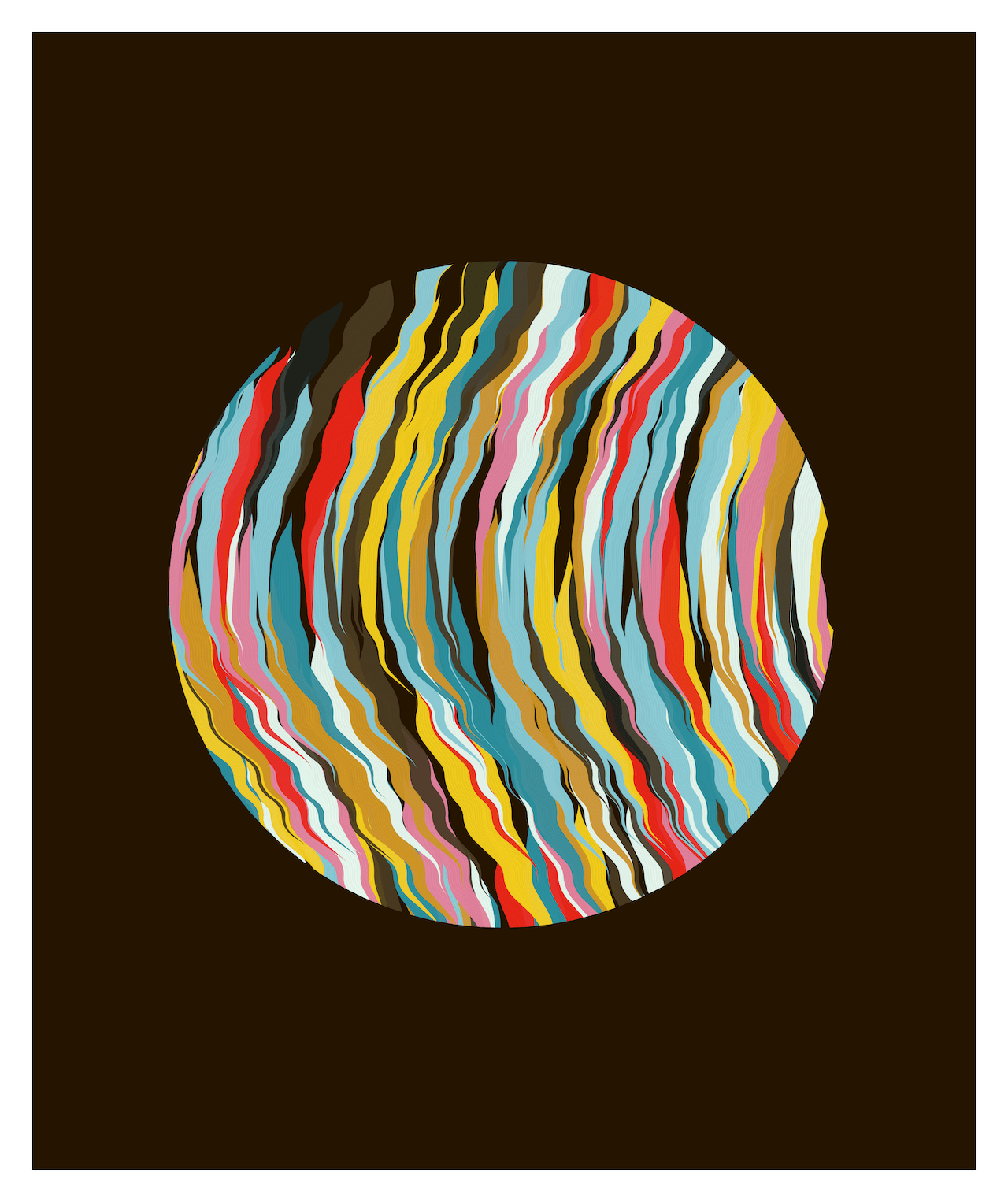
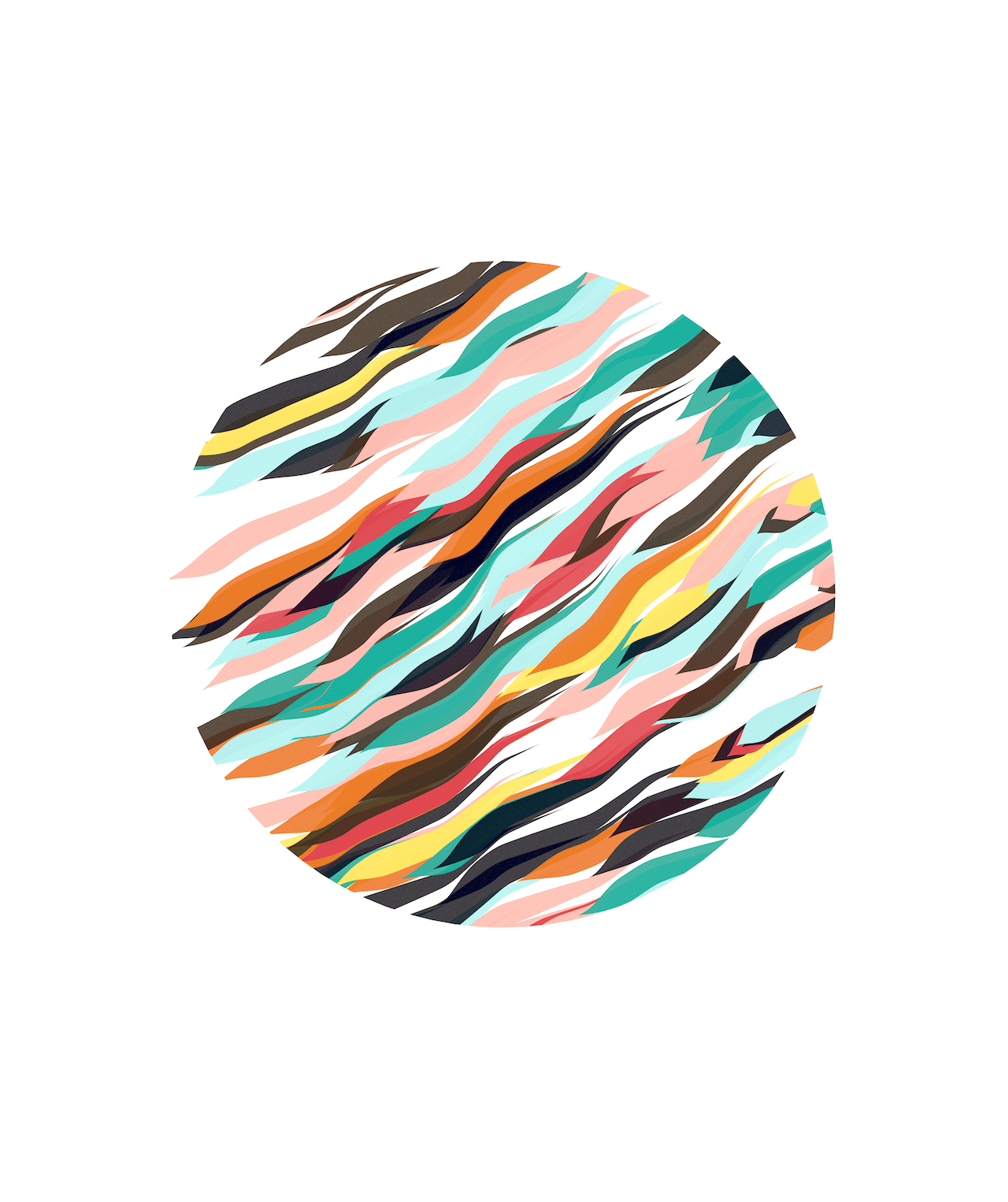
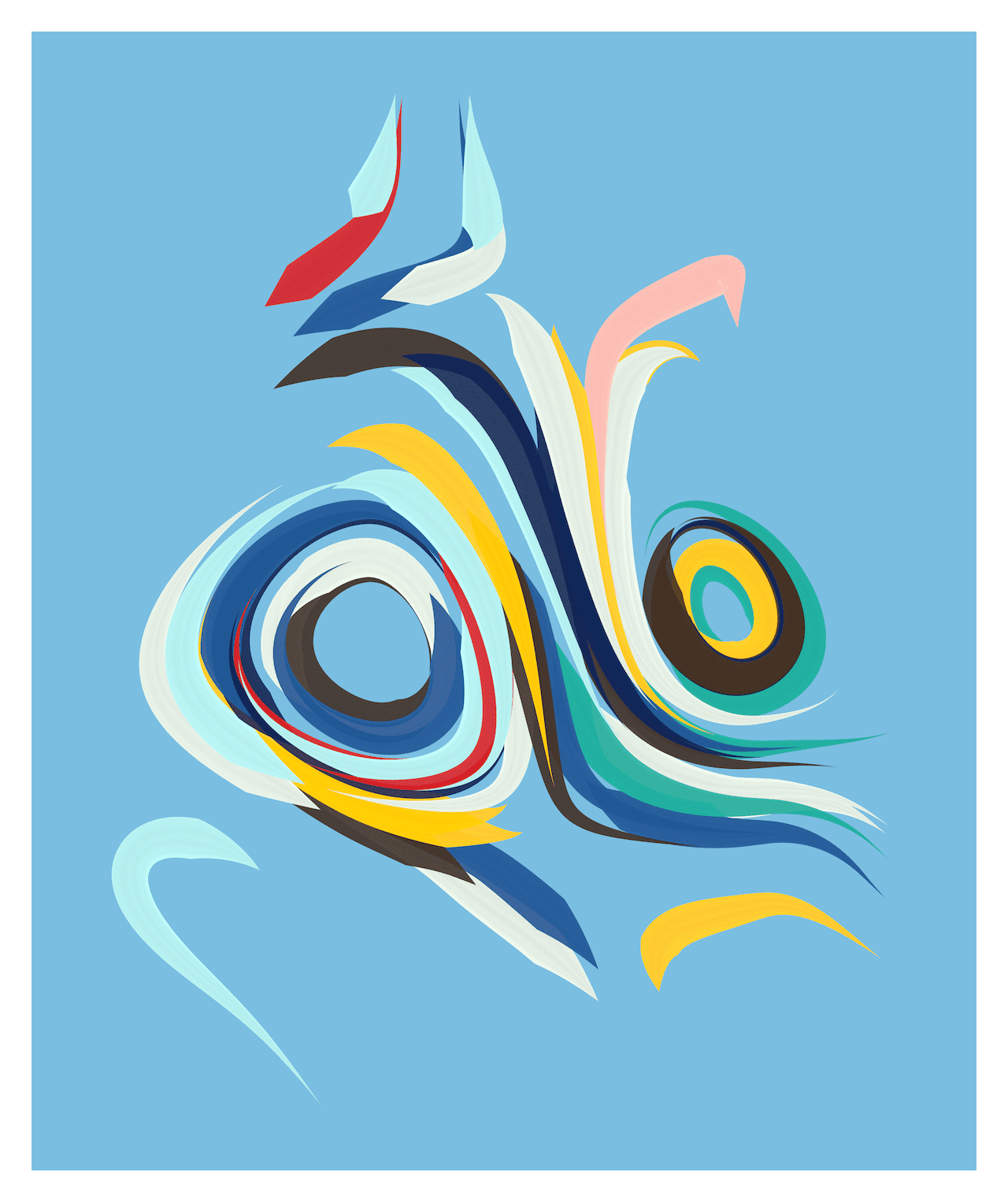
The Generative Process

October 2021 - 5 minute read

Introduction

Z-huge is my first blockchain project. Named in reference to the robotic oxen of Zhuge Liang.

It's been a real challenge to make every output from this work feel special, while being generated endlessly from the same code.

For prior generative work, I'd generate hundreds and choose only a handful of outputs, but for this project, I really wanted every output to feel hand-crafted.

To achieve this, most of the time spent on this work has gone into refining the bounds that the values can explore during generation. It feels a lot like carving at times, exploring seed values and combinations of properties that feel good, then establishing limits for the generation to explore.

Each mint is entirely unique, and each piece is non-fungible in its own right. Even with access to the source code, using the same seed value again will generate unique variations that mean each output is entirely (to a high level of entropy) unique.

Once all 512 of these are sold, there will be no further generation of Z-huge works.

I've been consistenly surpised by this process's output over the last few months, and I hope you love them.

The Noise

The underlying structure of the pieces is 2d curl noise. A perlin noise-based image is generated with some modifications to avoid 'guttering' - particularly strong areas that will suck in and trap our line-stepping function.

This data is read out as vectors, but I've visualised it below as visible tone.

Various processing passes are used to manipulate the noise field. These processing passes help create areas of sparseness or contrast that encourage the lines to behave differently and can tune the noise to create smoother, noisier and even chaotic patterns.

A somewhat naiive analysis runs after the noise is generated to check for interesting features of the noise (contrast, dynamic range) and the noise will be re-generated or transformed if these checks won't satisfy the seed value's intention. This can be quite an expensive (computationally) part of the generation process.

The Lines

Next, vector lines are stepped through the noise field, calculated with a curl function for each step.

Imagine you are standing on a mountain. You can see which way is uphill, and which way is downhill, but you want to choose to stay as flat as possible while still walking forwards. The only way to do this is to follow the path around the mountain. This takes your walk around the curvature of the mountain, like following the lines in a topographical map. Optionally, you may be given instruction to move up, or down the hill slightly, and your map may not be the exact same as your neighbour's map.

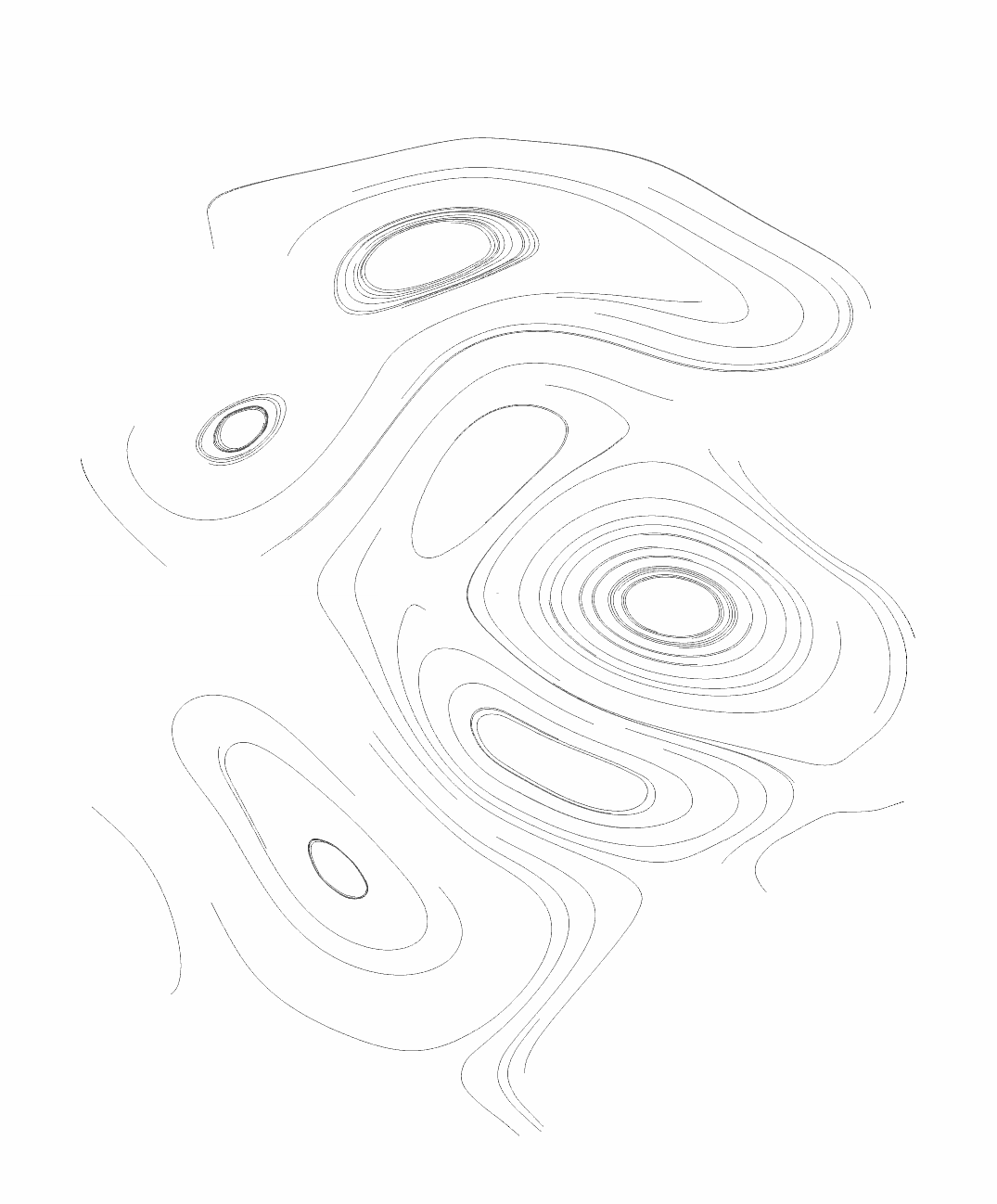
Lines are started at 'interesting' areas within the noise field, or based on one of many seed patterns. Often, this will create quite a few too many closely packed lines, so stepping through each, there's an optional check to see if they come in close proximity or overlap. Some of these are then optionally deleted or shortened depending on the seed value. Othertimes, they're left to intersect and overlap.

The Paint

Now we have a foundation, it's time to paint our lines. The lines are painted by laying out geometry at a variable width around each line. Colours are chosen probablistically from one of the 9 palettes.

The line width can also be varied along the length. This is informed by the seed value, but can also be influenced by the number of surrounding lines (depending on the initial seed value).

The Composition

Finally, we're ready to assemble the image. The bounds of our geometry are calculated and fit into our canvas - this ensures we've filled as much of our canvas as needed (and also covers up some mistakes).

The number of lines, noisiness, line profile and form are used to determine how the final image should be presented. A circular or square crop are used for more complex generations where the complexity can easily become overwhelming rather than pleasant. More simple structures like the one above are left un-cropped, this happens when more of the lines have been removed.

The Output

Your output is rendered at 6400 × 7629 and is suitable for an A4 print at 600dpi and up to an A2 print at 300dpi.